Mathematical Gems from Philip Lloyd.
Philip Lloyd has been a very successful mathematics teacher in New Zealand since 1967.
Philip Lloyd has been a very successful mathematics teacher in New Zealand since 1967.
Philip's personal guiding principle or philosophy:
To teach Mathematics using REASONS not RULES.
Mathematics must not be taught as “a set of rules to follow”.
It needs be taught with real understanding.
To teach Mathematics using REASONS not RULES.
Mathematics must not be taught as “a set of rules to follow”.
It needs be taught with real understanding.
There is a big difference between:
“Knowing” a thing and “Understanding” it.
For example, most students “know” that 2 to the power 0 = 1
but few “understand” WHY it is 1
Click on: https://youtu.be/rG2io0ht_EE
“Knowing” a thing and “Understanding” it.
For example, most students “know” that 2 to the power 0 = 1
but few “understand” WHY it is 1
Click on: https://youtu.be/rG2io0ht_EE
To INSPIRE students the secret is......ENTHUSIASM!
A teacher needs to be enthusiastic all the time!
ENTHUSIASM IS CONTAGIOUS!
ENTHUSIASM CREATES ENERGY!
ENTHUSIASM IS THE KEY TO SUCCESS IN EVERY ACTIVITY!
A teacher needs to be enthusiastic all the time!
ENTHUSIASM IS CONTAGIOUS!
ENTHUSIASM CREATES ENERGY!
ENTHUSIASM IS THE KEY TO SUCCESS IN EVERY ACTIVITY!
The following links are a collection of special gems which illuminate real understanding of concepts which are too often glossed over in most texts.
1. Understanding Differentiation of Powers of x.
Click HERE for animated PowerPoint which will delight students.
Click for video: https://youtu.be/Gpv7dAXnfsE
Click HERE for animated PowerPoint which will delight students.
Click for video: https://youtu.be/Gpv7dAXnfsE
2. The Derivative of e to the power of x.
Click on: https://youtu.be/DYZf4dGhESY
Also click on:https://youtu.be/YRKOd0Hb_Po
Click on: https://youtu.be/DYZf4dGhESY
Also click on:https://youtu.be/YRKOd0Hb_Po
3. Volume of a PYRAMID
Click HERE for a PowerPoint showing a CUBOID turning into 3 PYRAMIDS.
Click for video: https://youtu.be/T-G49JUQAdA
Click HERE for a PowerPoint showing a CUBOID turning into 3 PYRAMIDS.
Click for video: https://youtu.be/T-G49JUQAdA
4. The RELATIVE SIZES and position of Earth, Moon and Sun.
Click HERE for a simple way of comparing HUGE distances. How many people realise that the distance from the earth to the moon is only about a third of the distance across the sun?
Click HERE for a simple way of comparing HUGE distances. How many people realise that the distance from the earth to the moon is only about a third of the distance across the sun?
5. Drawing graphs of gradient functions
and drawing functions from their gradient graphs.
Click HERE for a clear and comprehensive treatment of this quite complex topic. The booklet contains student practice sheets and answer sheets.
and drawing functions from their gradient graphs.
Click HERE for a clear and comprehensive treatment of this quite complex topic. The booklet contains student practice sheets and answer sheets.
6. The vanishing points of inflection.
The strange function in this section has a second derivative of zero at x = 1 and seems to be quite normal, but it does not have a point of inflection! The full story is far more complicated and fascinating.
Click on video
https://youtu.be/amISGfrci0k
THEORY
https://youtu.be/zkYMO8XLXzc
Click for additional introductory videos:
POINTS OF INFLECTION 1
https://youtu.be/sEh9_khIqcQ
-----------------------------------------------------------------------------------------------
POINTS OF INFLECTION 2
https://youtu.be/sapXFeIQMgg
-----------------------------------------------------------------------------------------------
POINTS OF INFLECTION 3
https://youtu.be/XuLQ-jy3070
=========================================================
VANISHING POINTS OF INFLECTION for y = x^4
https://youtu.be/lga-SPIf634
Click HERE for a printable version.
The strange function in this section has a second derivative of zero at x = 1 and seems to be quite normal, but it does not have a point of inflection! The full story is far more complicated and fascinating.
Click on video
https://youtu.be/amISGfrci0k
THEORY
https://youtu.be/zkYMO8XLXzc
Click for additional introductory videos:
POINTS OF INFLECTION 1
https://youtu.be/sEh9_khIqcQ
-----------------------------------------------------------------------------------------------
POINTS OF INFLECTION 2
https://youtu.be/sapXFeIQMgg
-----------------------------------------------------------------------------------------------
POINTS OF INFLECTION 3
https://youtu.be/XuLQ-jy3070
=========================================================
VANISHING POINTS OF INFLECTION for y = x^4
https://youtu.be/lga-SPIf634
Click HERE for a printable version.
7. Those essential SPECIAL TRIANGLES.
To really grasp these useful ideas, students need to know how they are formed.
Click on https://youtu.be/JSwY9hMGgXk
Click HERE for a printable version.
To really grasp these useful ideas, students need to know how they are formed.
Click on https://youtu.be/JSwY9hMGgXk
Click HERE for a printable version.
8. Centres of a Triangle.
The centroid, circumcentre and orthocentre are closely related.
Click on https://www.screencast.com/t/OzOoH2SotIfB
to see a moving demonstration of how these centres can vary and merge.
The centroid, circumcentre and orthocentre are closely related.
Click on https://www.screencast.com/t/OzOoH2SotIfB
to see a moving demonstration of how these centres can vary and merge.
9. Clock-face Polygons.
For a demonstration of this instructional investigation for young students of geometry.
Click on https://www.screencast.com/t/vR0gPQEgq7v
Click HERE for a printable version with worksheets for student investigation.
Click HERE for blank clock faces.
Click HERE for answer sheet.
For a demonstration of this instructional investigation for young students of geometry.
Click on https://www.screencast.com/t/vR0gPQEgq7v
Click HERE for a printable version with worksheets for student investigation.
Click HERE for blank clock faces.
Click HERE for answer sheet.
10 THE FAMOUS "SPIDER AND FLY PROBLEM".
This would be one of my all-time favourite lessons!
Click HERE for a printable version for teaching notes.
This would be one of my all-time favourite lessons!
Click HERE for a printable version for teaching notes.
11 Millionaire Hotseat (PPT) on Pythagoras
To start the PowerPoint press function key F5
To start the PowerPoint press function key F5
12 Millionaire Hotseat (PPT) on Trigonometry
To start the PowerPoint press function key F5
To start the PowerPoint press function key F5
13. LLOYD’S FORMULA
for the area of any triangle with sides a, b, c.
Click HERE for a printable version of this original idea.
for the area of any triangle with sides a, b, c.
Click HERE for a printable version of this original idea.
14. A “tongue in cheek” article on the misuse of graphics calculators.
Click HERE for a printable version of this article.
Click HERE for a printable version of this article.
15. “CAN’T GET NO SATISFACTION”.
Click HERE for a printable version of this article about doing things the “thinking way” verses the “non-thinking way”.
Click HERE for a printable version of this article about doing things the “thinking way” verses the “non-thinking way”.
16. WHY BOTHER WITH RADIANS IN YEAR 12 MATHEMATICS?
Click HERE for a printable version of this thought provoking
article.
Click HERE for a printable version of this thought provoking
article.
17. INTRIGUING CONTINUED FRACTIONS.
Click HERE to see how a sequence of continued fractions can apparently produce irrational and imaginary numbers!
Click HERE to see how a sequence of continued fractions can apparently produce irrational and imaginary numbers!
18. SUPERB INVESTIGATION SUITABLE AT MANY LEVELS.
Click HERE for teacher’s notes on an investigation that could be started even with juniors but ends up as a senior calculus problem.
Click HERE for teacher’s notes on an investigation that could be started even with juniors but ends up as a senior calculus problem.
19. STATIONARY SATELLITES. Did you know that communications satellites circle the earth at a distance of about 36,000 kilometres above the equator AND they stay above particular points on the equator?
Click HERE for a poster giving the reasoning and information. GEO-STATIONARY SATELLITES Video
CLICK HERE https://www.screencast.com/t/aWy40oGYCdMm
Click HERE for a poster giving the reasoning and information. GEO-STATIONARY SATELLITES Video
CLICK HERE https://www.screencast.com/t/aWy40oGYCdMm
20. SOME FORMULAS THAT ACTUALLY DO REAL STUFF!
Find how high you can throw a ball just by timing it;
Find how far away the horizon is at different heights;
Find how fast you would drive round a corner before the car rolls;
Find what speed would make you airborne going over a hump-back bridge;
Find how far motor cycles can jump off ramps; and more!
Click HERE
Find how high you can throw a ball just by timing it;
Find how far away the horizon is at different heights;
Find how fast you would drive round a corner before the car rolls;
Find what speed would make you airborne going over a hump-back bridge;
Find how far motor cycles can jump off ramps; and more!
Click HERE
1. Click HERE for PRIMARY VALUES OF INDICES.
Did YOU know that the cube root of (-8) does not equal -2?
Also view the VIDEO by clicking
https://youtu.be/fAe34f8UdKU
22. From FLATLAND to the 4th DIMENSION.
See video: https://youtu.be/jPrnU009IA8
Click HERE to see the document.
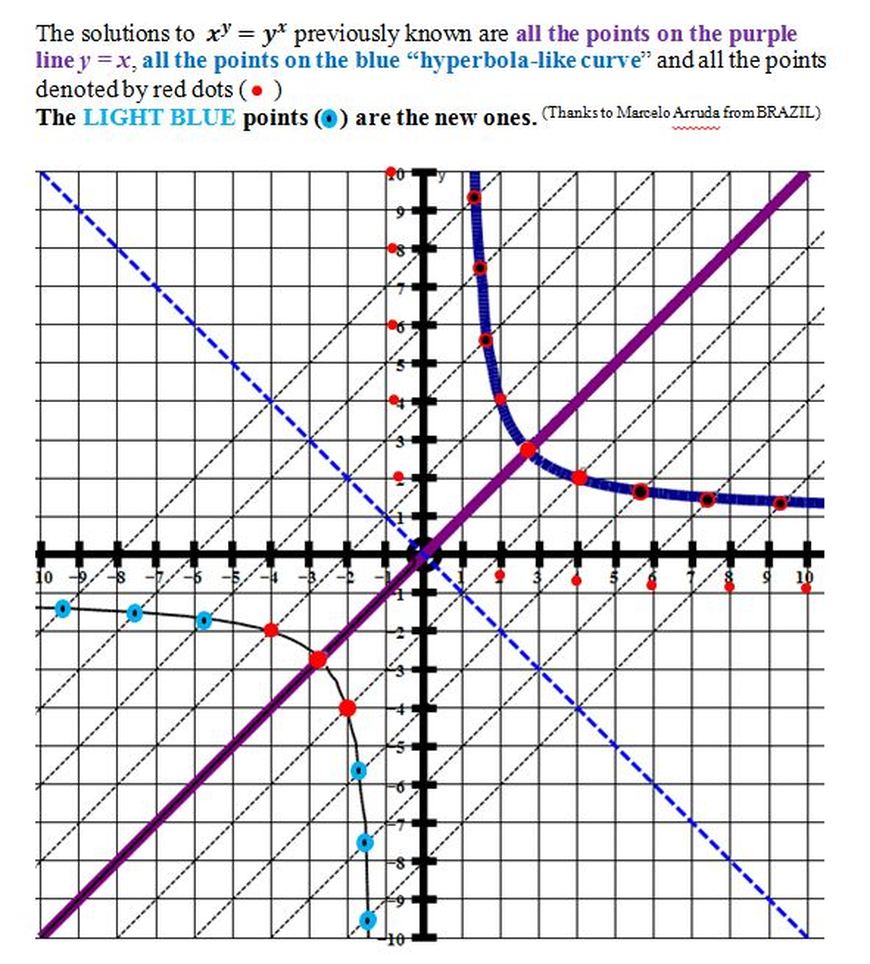
23. Finding solutions to y^x =x^y
Click HERE for the theory.
Click HERE for a new set of solutions found by Marcelo Arruda from Brazil.
Did YOU know that the cube root of (-8) does not equal -2?
Also view the VIDEO by clicking
https://youtu.be/fAe34f8UdKU
22. From FLATLAND to the 4th DIMENSION.
See video: https://youtu.be/jPrnU009IA8
Click HERE to see the document.
23. Finding solutions to y^x =x^y
Click HERE for the theory.
Click HERE for a new set of solutions found by Marcelo Arruda from Brazil.
24. Special Angles between the Hour Hand and the
Minute Hand of a clock.
Click HERE
25. Can passenger jets fly backwards?
Click HERE
26. The GOLDEN RECTANGLE.
Click HERE
27. Problems with the “Fundamental Theorem of Algebra”.
Click HERE
Watch these videos:
y=( x – 1)^2 + c showing complex roots
https://youtu.be/gXxUJA01qfY
==============================================
(Phantom Graphs) Cubics always have 3 roots
https://youtu.be/5KQF4OQhmQw
SHOWING TYPICAL QUARTIC ALWAYS HAS 4 solutions
https://youtu.be/XQ1uRsMet60
QUARTIC CURVE with DETACHING PHANTOMS
https://youtu.be/jd_BFXAG8xc
FUNDAMENTAL THEOREM OF ALGEBRA using Quintic Curve
https://youtu.be/ug9gv8CMWUs
CUBIC WITH DETACHING PHANTOMS *
https://youtu.be/Wq_SFJ9hSfY
QUARTIC CURVE with DETACHING PHANTOMS
https://youtu.be/jd_BFXAG8xc
28. Converting between Fahrenheit and Celsius temperature scales Mentally.
Click HERE
29. Teaching "Order of Operations" logically.
click HERE
30. Teaching DIVISION of FRACTIONS.
click HERE
Here is a short video covering the above ideas…
https://youtu.be/_zsVyZ9BVA4
31. The NEWTON-RAPHSON Method.
click HERE
32. Does √(a×b) always equal √(a) ×√(b) ?
click HERE
33. The graph of y = x^x
click HERE
video: https://youtu.be/VEGpOvT3tPE
34. Why is the cube root of -1 not equal to -1?
click HERE
35. Implicit Differentiation explained.
click HERE
36. What do I need to know before the BINOMIAL THEOREM?
click HERE
37. How can sin(x) equal -2?
click HERE
38. How can e^x be negative?
click HERE
39. How can there be 4 intersections for the graphs y = x^2 and x^2 + y^2 = 1? click HERE
40. Why is it that when f''(x) = o this represents a point of inflection on the curve y=f(x) click HERE
41. Trisecting an angle!
click HERE
42. The amazing graph of y = (-1)^x
click HERE
VIDEO: https://youtu.be/iLgBmglVPsQ
43. Why can't we differentiate a power of x and get 1/x ?
click HERE
44. Why is sin(90) equal to 1 ?
click HERE
The TRIGOMETER
Videos: https://youtu.be/LFj4UQHlCQw
Showing how sin, cos and tan are defined
https://youtu.be/TAq3yKlumms
45. A simple intersection problem that turned out to be not so simple!
click HERE
46. What is an inverse function?
click HERE
47. How can there be TWO angles of projection which will result in the same range for a projectile?
click HERE
48. What’s the point of radians? Why don’t we just write everything in degrees?
click HERE
49. Why isn’t math taught in a way that if you know how to do the problems you will get it right even if you make a simple mistake?
click HERE
50. Why can’t we fold a piece of paper more than eight times?
click HERE
51. Intersecting Circles with an astonishing conclusion!
click HERE
52. Some probability problems using tree diagrams and Venn
diagrams.
(a) If the probability that a problem will be solved by three people is 1/2, 1/3 and 1/6, then what
is the probability that the problem will be solved? CLICK HERE
(b) A bag contains 5 white and 3 black balls, and two balls are drawn at random. What is the
probability that both are different colours? CLICK HERE
(c) If n(A) =22, n(B) =32 and n(AUB) =40, what is the value of n(A∩B) CLICK HERE
(d) If P(A) =0.65 and P(B) =0.35 and P(A∩B) =0.1 what is the P(B|A) CLICK HERE
(e) What is the probability of picking a red marble and heads simultaneously from a basket which
has 5 blue marbles. CLICK HERE
53. THE WORLD’S HARDEST EASY GEOMETRY QUESTION. CLICK HERE
TO BE CONTINUED!!!
CONTACT PHILIP LLOYD (Specialist Calculus Teacher) by email IF YOU DECIDE TO USE ANY OF MY RESOURCES I WOULD BE PLEASED IF YOU COULD SEND ME AN EMAIL.
[email protected]
See web sites:
http://www.linkedin.com/pub/philip-lloyd/2a/787/7a0
http://www.phantomgraphs.weebly.com
http://www.intersectingplanes.weebly.com
http://trigometer.weebly.com
http://mathematicalgems.weebly.com
http://knowingisnotunderstanding.weebly.com
http://calculusresources.weebly.com
http://algebra-and-calculus-resources-year12.weebly.com
http://liveperformances.weebly.com/
http://www.motivational-and-inspirational-sayings.weebly.com
http://motivation-and-self-esteem-cycles.weebly.com
Enthusiasm is the key to success in every activity!
[email protected]
See web sites:
http://www.linkedin.com/pub/philip-lloyd/2a/787/7a0
http://www.phantomgraphs.weebly.com
http://www.intersectingplanes.weebly.com
http://trigometer.weebly.com
http://mathematicalgems.weebly.com
http://knowingisnotunderstanding.weebly.com
http://calculusresources.weebly.com
http://algebra-and-calculus-resources-year12.weebly.com
http://liveperformances.weebly.com/
http://www.motivational-and-inspirational-sayings.weebly.com
http://motivation-and-self-esteem-cycles.weebly.com
Enthusiasm is the key to success in every activity!